Empowerment
Empowerment is a mathematical expression that includes two terms called: ay base exponent n.
He writes and reads: Its definition varies according to the numerical set that belongs to the exponent:
• When the exponent is a natural number, is to multiply a number by itself several times: the exponent determines the number of times.
• when the exponent is a negative integer is equivalent to the inverse fraction of the base but with positive exponent.
.
Any number raised to 0 is equivalent to 1 except the particular case of 00 which, in principle, is an uncertainty (see zero).
The definition of empowerment can be extended to real exponents, complex or matrix.
Properties of empowerment
power exponent 0
power exponent 1
output powers equal basis
Ratio Base Equal Powers Power of a product
Power of a power
Distributive
properties not meeting the empowerment
power base 10
Power of complex numbers
Figure
See also
External links
Properties of empowerment
Enhancing properties are what allow different methods to resolve a power. These are:
Power exponent 0
One definition of empowerment, by recursion, as follows:
If the second expression is taken a = 1, we have that x Dividing the two terms of the equation by x (which can be done whenever x is not 0), is that x0 = 1.
Thus, every power base exponent 0 and different from 0 is equal to 1
but must belong to the real
Power exponent 1
All power exponent 1 is equal to the base.
Product of powers of equal base
The product of two or more powers equal basis is equal to the power exponent ay base equal to the sum of the corresponding exponents. Place the same base and add the exponents:
Equal Powers Ratio Base
The division of two equal power base is equal to the basic power exponent equal to and subtracted from the respective exponents. Place the same database and are subtracted
Power of a product
The potency of a product is equal to each of the factors of the product raised to an exponent of that power. That is, a power base (ab) and the exponent "n" equals the factor "a" raised to "n" by the factor "b" raised to "n".
Power of a power
The power of a power base is equal to the power base raised to the multiplication of both exponents. Place the same base and multiply the exponents. This gives this power
Distributive
Empowerment is distributive with respect to multiplication and division, but it's not about the sum or subtraction.
Is distributive with respect to multiplication and division:
Properties not meeting the empowerment
It is distributive over addition and subtraction:

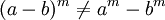
Commutative property does not meet except in cases where base and exponent are of equal value or equivalent. Overall.
Power base 10
Normally, the powers with base 10, by the amount representing the exponent, that is the number of zeros in the result. The rest of the base, to get the result the number is multiplied by itself many times indicate the exponent. Example:
10^2=100. 10^5=100.000
Power of complex numbers
For any real numbers have the identity: